
En matemáticas, una matriz es una tabla de números consistente en cantidades abstractas que pueden sumarse y multiplicarse. Las matrices se utilizan para
describir sistemas de ecuaciones lineales, realizar un seguimiento de los coeficientes de una aplicación lineal y registrar los datos que dependen de varios parámetros. Las matrices se describen en el campo de la teoría de matrices. Pueden sumarse, multiplicarse y descomponerse de varias formas, lo que también las hace un concepto clave en el campo del álgebra lineal.
Definiciones y notaciones
Una matriz es una tabla cuadrada o rectangular de datos (llamados elementos o entradas de la matriz) ordenados en filas y columnas, donde una fila es cada una de las líneas horizontales de la matriz y una columna es cada una de las líneas verticales. A una matriz con m filas y n columnas se le denomina matriz m-por-n (escrito m×n), y a m y n dimensiones de la matriz. Las dimensiones de una matriz siempre se dan con el número de filas primero y el número de columnas después. Comúnmente se dice que una matriz m-por-n tiene un orden de m × n ("orden" tiene el significado de tamaño). Dos matrices se dice que son iguales si son del mismo orden y tienen los mismos elementos. Al elemento de una matriz que se encuentra en la fila i-ésima y la columna j-ésima se le llama elemento i,j o elemento (i,j)-iésimo de la matriz. Se vuelve a poner primero las filas y después las columnas.
Casi siempre, se denotan a las matrices con letras mayúsculas mientras que se utilizan las correspondientes letras en minúsculas para denotar a los elementos de las mismas. Por ejemplo, al elemento de una matriz A que se encuentra en la fila i-ésima y la columna j-ésima se le denota como ai,j o a[i,j]. Notaciones alternativas son A[i,j] o Ai,j. Además de utilizar letras mayúsculas para representar matrices, numerosos autores representan a las matrices con fuentes en negrita para distinguirlas de otros tipos de variables. Así A es una matriz, mientras que A es un escalar.
Normalmente se escribe para definir una matriz A m × n con cada entrada en la matriz A[i,j] llamada aij para todo 1 ≤ i ≤ m y 1 ≤ j ≤ n. Sin embargo, la convención del inicio de los índices i y j en 1 no es universal: algunos lenguajes de programación comienzan en cero, en cuál caso se tiene 0 ≤ i ≤ m − 1 y 0 ≤ j ≤ n − 1.
para definir una matriz A m × n con cada entrada en la matriz A[i,j] llamada aij para todo 1 ≤ i ≤ m y 1 ≤ j ≤ n. Sin embargo, la convención del inicio de los índices i y j en 1 no es universal: algunos lenguajes de programación comienzan en cero, en cuál caso se tiene 0 ≤ i ≤ m − 1 y 0 ≤ j ≤ n − 1.
 para definir una matriz A m × n con cada entrada en la matriz A[i,j] llamada aij para todo 1 ≤ i ≤ m y 1 ≤ j ≤ n. Sin embargo, la convención del inicio de los índices i y j en 1 no es universal: algunos lenguajes de programación comienzan en cero, en cuál caso se tiene 0 ≤ i ≤ m − 1 y 0 ≤ j ≤ n − 1.
para definir una matriz A m × n con cada entrada en la matriz A[i,j] llamada aij para todo 1 ≤ i ≤ m y 1 ≤ j ≤ n. Sin embargo, la convención del inicio de los índices i y j en 1 no es universal: algunos lenguajes de programación comienzan en cero, en cuál caso se tiene 0 ≤ i ≤ m − 1 y 0 ≤ j ≤ n − 1.Una matriz con una sola columna o una sola fila se denomina a menudo vector, y se interpreta como un elemento del espacio euclídeo. Una matriz 1 × n (una fila y n columnas) se denomina vector fila, y una matriz m × 1 (una columna y m filas) se denomina vector columna.
La matriz,

es una matriz 4x3. El elemento A[2,3] o a2,3 es 7.
La matriz,
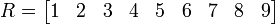
es una matriz 1×9, o un vector fila con 9 elementos.
OPERACIONES BASICAS
Suma o adición:
Dadas las matrices m-por-n ,A y B, su suma A + B es la matriz m-por-n calculada sumando los elementos correspondientes (i.e. (A + B)[i, j] = A[i, j] + B[i, j] ). Es decir, sumar cada uno de los elementos homólogos de las matrices a sumar. Por ejemplo:
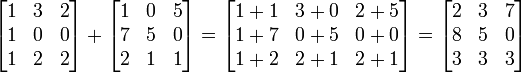
PROPIEDADES
Asociativa:
Dadas las matrices m×n A, B y C
A + (B + C) = (A + B) + C
Conmutativa:
Dadas las matrices m×n A y B
A + B = B + A
Existencia de matriz cero o matriz nula:
A + 0 = 0 + A = A
Existencia de matriz opuesta:
con gr-A = [-aij]
A + (-A) = 0
PRODUCTO POR UN ESCALAR
Dada una matriz A y un escalar c, su producto cA se calcula multiplicando el escalar por cada elemento de A (i.e. (cA)[i, j] = cA[i, j] ).
Ejemplo:
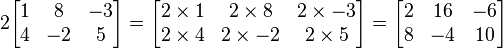
PROPIEDADES
Sean A y B matrices y c y d escalares.
Clausura: Si A es matriz y c es escalar, entonces cA es matriz.
Asociatividad: (cd)A = c(dA)
Elemento Neutro: 1·A = A
Distributividad:
De escalar: c(A+B) = cA+cB
De matriz: (c+d)A = cA+dA

PRODUCTO
El producto de dos matrices se puede definir sólo si el número de columnas de la matriz izquierda es el mismo que el número de filas de la matriz derecha. Si A es una matriz m×n y B es una matriz n×p, entonces su producto matricial AB es la matriz m×p (m filas, p columnas) dada por:
![(AB)[i,j] = A[i,1] B[1,j] + A[i,2] B[2,j] + ... + A[i,n] B[n,j] \!\](http://upload.wikimedia.org/math/3/6/8/3685038eaea4a600957beea930ad474c.png)
para cada par i y j.
Por ejemplo:

MATRICES CUADRADAS Y DEFINICIONES RELACIONADAS
Una matriz cuadrada es una matriz que tiene el mismo número de filas que de columnas. El conjunto de todas las matrices cuadradas n-por-n junto a la suma y la multiplicación de matrices, es un anillo que generalmente no es conmutativo.
M(n,R), el anillo de las matrices cuadradas reales, es un álgebra asociativa real unitaria. M(n,C), el anillo de las matrices cuadradas complejas, es un álgebra asociativa compleja.
La matriz identidad In de orden n es la matriz n por n en la cual todos los elementos de la diagonal principal son iguales a 1 y todos los demás elementos son iguales a 0. La matriz identidad se denomina así porque satisface las ecuaciones MIn = M y InN = N para cualquier matriz M m por n y N n por k. Por ejemplo, si n = 3:
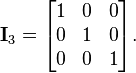
La matriz identidad es el elemento unitario en el anillo de matrices cuadradas.
Los elementos invertibles de este anillo se llaman matrices invertibles o matrices no singulares. Una matriz A n por n es invertible si y sólo si existe una matriz B tal que
AB = In = BA.
En este caso, B es la matriz inversa de A, identificada por A-1 . El conjunto de todas las matrices invertibles n por n forma un grupo (concretamente un grupo de Lie) bajo la multiplicación de matrices, el grupo lineal general.
Si λ es un número y v no es un vector nulo tal que Av = λv, entonces se dice que v es un vector propio de A y que λ es su valor propio asociado. El número λ es un valor propio de A si y sólo si A−λIn no es invertible, lo que sucede si y sólo si pA(λ) = 0, donde pA(x) es el polinomio característico de A. pA(x) es un polinomio de grado n y por lo tanto, tiene n raíces complejas múltiples raíces si se cuentan de acuerdo a su multiplicidad. Cada matriz cuadrada tiene como mucho n valores propios complejos.
El determinante de una matriz cuadrada A es el producto de sus n valores propios, pero también puede ser definida por la fórmula de Leibniz. Las matrices invertibles son precisamente las matrices cuyo determinante es distinto de cero.
El algoritmo de eliminación gaussiana puede ser usado para calcular el determinante, el rango y la inversa de una matriz y para resolver sistemas de ecuaciones lineales.
La traza de una matriz cuadrada es la suma de los elementos de la diagonal, lo que equivale a la suma de sus n valores propios.























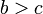 entonces
entonces 
 entonces
entonces 
 entonces
entonces  y
y 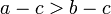
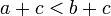 y
y 
 es positivo y
es positivo y  y
y 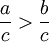
 y
y 